1. Introduction
Recently, there has been substantial demand for high-capacity Li secondary batteries to meet the needs of electric vehicles and energy storage systems as well as mobile IT devices. For this reason, many research groups tried to enhance the battery performances by exploring alternatives to the core materials, while the main efforts of the battery manufacturers have been applied for modification of existing materials and cell design optimization of internal spaces. Among the alternatives, Si and Sn anodes have been researched intensively because of their high capacity and potential to overcome the theoretical capacity limit of commercialized graphite
[1-
8]. However, these high-capacity anodes undergo severe volume changes during the reaction, which brings critical problems in the key performance features such as cycling and reliability.
One of the typical phenomena of these anodes is the tendency to crack, and this crack propagation may cause an internal electric short. To solve these problems, many approaches, such as metal-carbon composites, thin-film electrodes, multiphase alloys, and active-nonreactive matrix, were employed, and remarkably improved results were achieved
[15-
18]. Among those approaches, the active-nonreactive matrix is known as one of the effective ways to suppress the cracking produced by volume changes
[2,
6-
13]. In previous studies on the active-nonreactive matrix, several research groups mainly adopted preparation methods of sputtering and mechanical alloying (MA) to optimize the electrochemical performance by controlling the elemental composition and/or the crystal structure
[15]. These methods have various advantages, such as convenience of compositional survey and relatively simple process parameters, but also have difficulties in control of sample quality, such as crystallinity, and in transfer to larger production scale. It was reported that the samples from these preparation methods are undesired amorphous or a mixture of amorphous and crystalline, despite the deliberate design
[15,
19]. Moreover, a composition produced by a method, such as sputtering, might not be materialized easily and thus may lead to misjudging the optimum composition for practical applications.
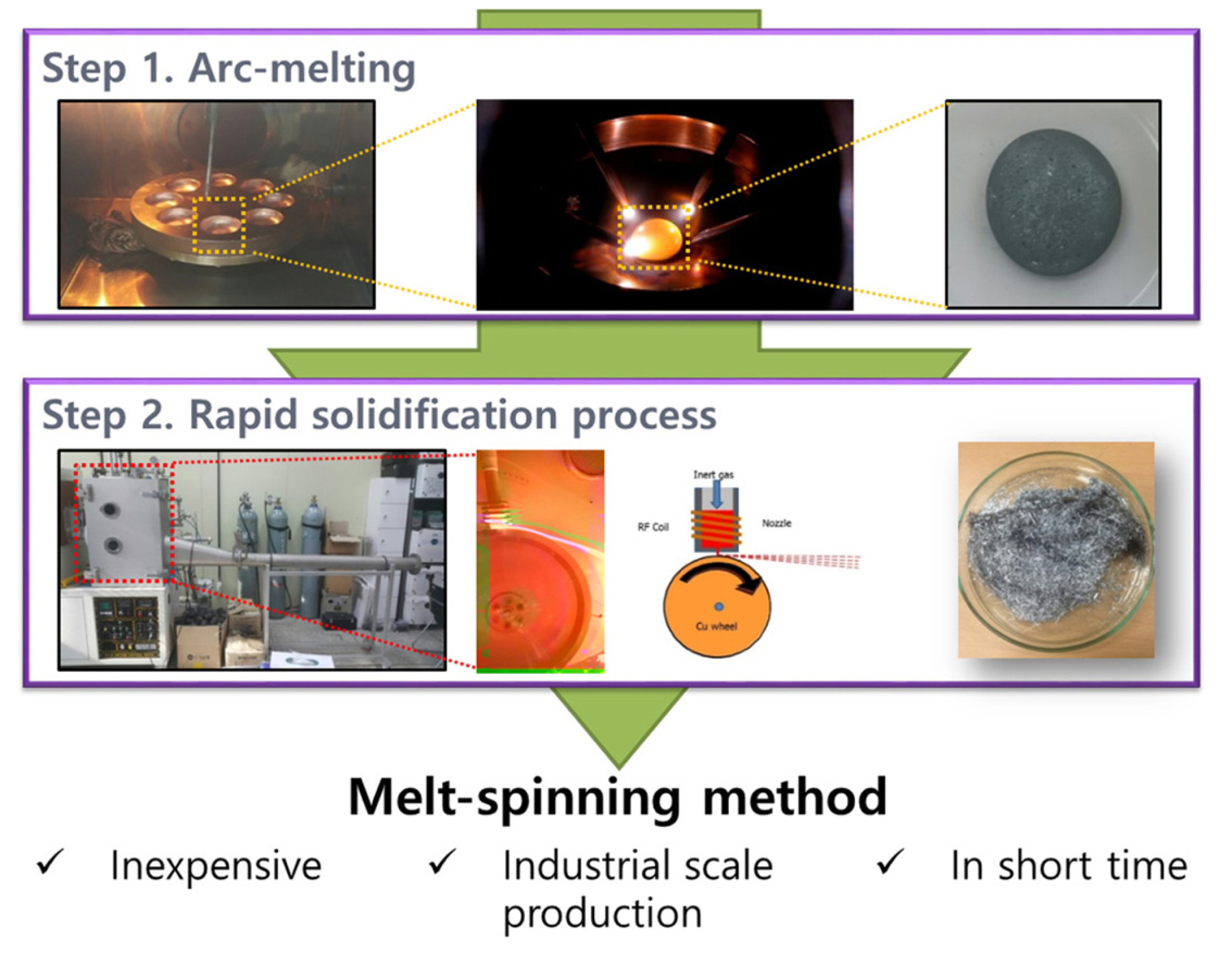
Here, we report a SiŌĆōFeŌĆōAl ternary alloy prepared by a facile and inexpensive process, melt spinning, which can control a certain level of solidification speed (around 10
3ŌĆō10
6 K/s), and is known as the most suitable method for the mass production of alloys
[16]. Another advantage of Si-alloys produced by the melt-spinning process is a tendency to be formed in the equilibrium state (most stable) as designed based on the phase diagram. As a rule, the phase diagram is very useful for metallurgists, material engineers, and material scientists to control the compositions and predict the phases of alloys under certain conditions. Therefore, the use of the phase diagram allows the design of alloys with required properties to be performed more efficiently and cost-effectively. In Li-ion batteries, as mentioned above, Si-based alloys are considered as the most promising anode material with the active/inactive matrix concept. Traditionally, by utilizing the phase diagram, we theoretically predict secondary phases formed along with active Si; however, their specific capacities should be practically measured. Thereby, the main purpose of this work is the development of a fundamental approach to predict specific capacities of Si-alloys in conjugation with the phase diagram. This prediction method can be used to efficiently design an alloy with a desired capacity without timeconsuming investigations of a large number of possible alloy compositions.
3. Results and Discussion
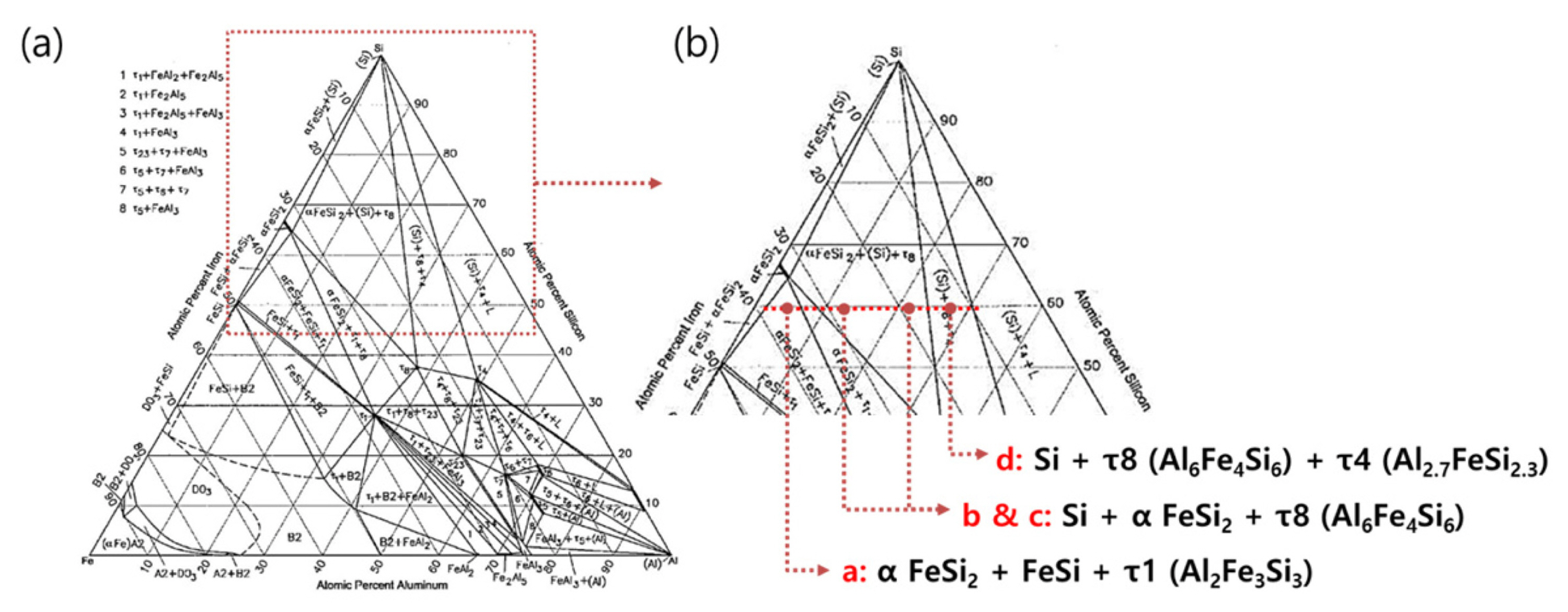
As shown in
Table 1, all samples have the same atomic percentage of Si with a varying ratio of Al and Fe, and therefore it might be assumed that they would have the same reaction amount of Li with Si. However, there are different amounts of active Si due to the formation of various intermetallic compounds such as FeŌĆōSi
x and Al
zŌĆōFe
yŌĆōSi
x as shown in
Fig. 1. We could infer that there is no active Si in the sample
a because sample
a is located in the three-phase coexistence region of FeSi, FeSi
2, and Al
2Fe
3Si
3 through the phase diagram. In the case of sample
b, in the region of Si, SiFe
2, and Al
6Fe
4Si
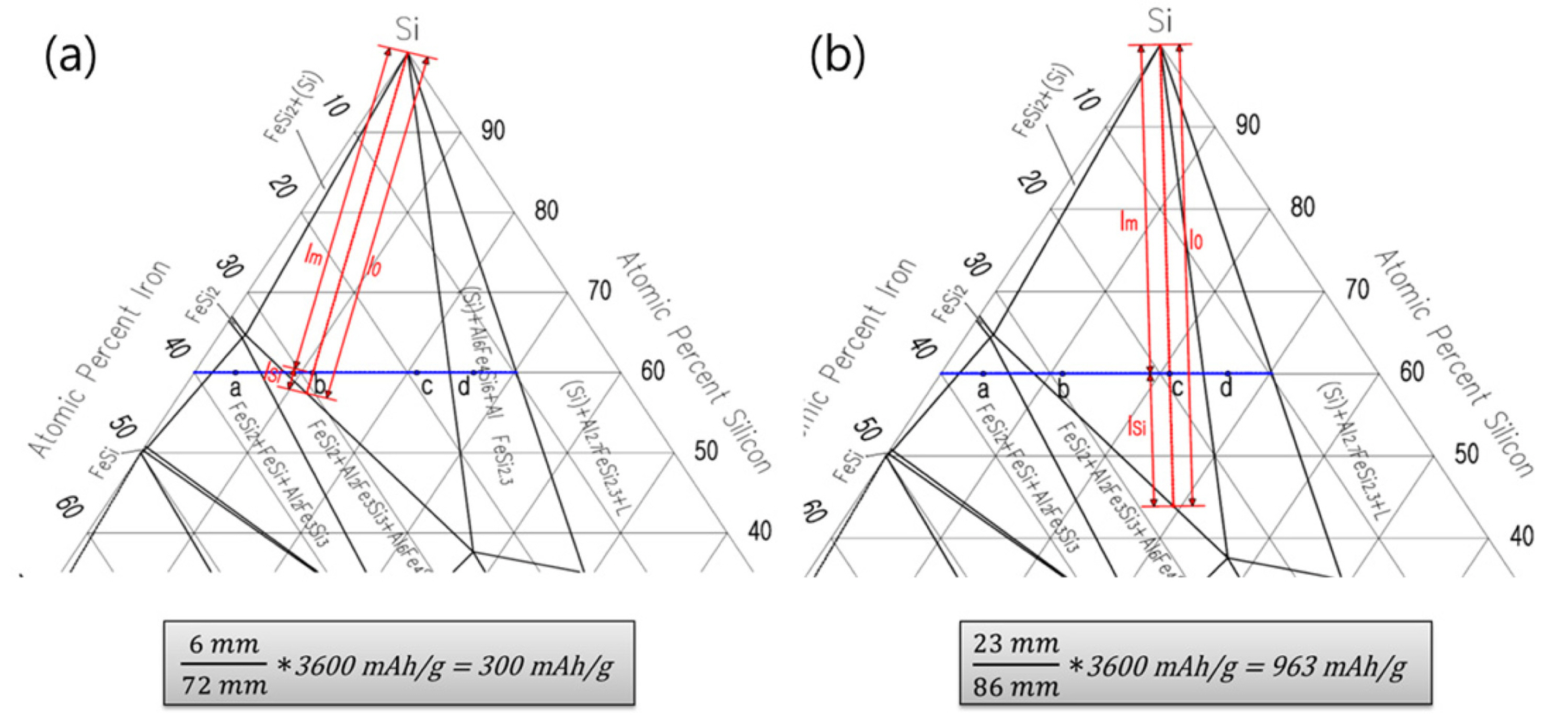
6, a capacity of 300 mAh/g might be expected by the lever rule of active Si (
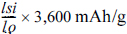
) as shown in
Fig. 3(a). The reversible reaction was assumed to be Li
3.75Si with an identical capacity of about 3600 mAh/g
[7,
14]. According to the same estimation procedure, the capacities of samples
c and
d were expected to be 963 mAh/g and 1368 mAh/g, respectively.
Fig. 3(b) shows the capacity estimation of sample
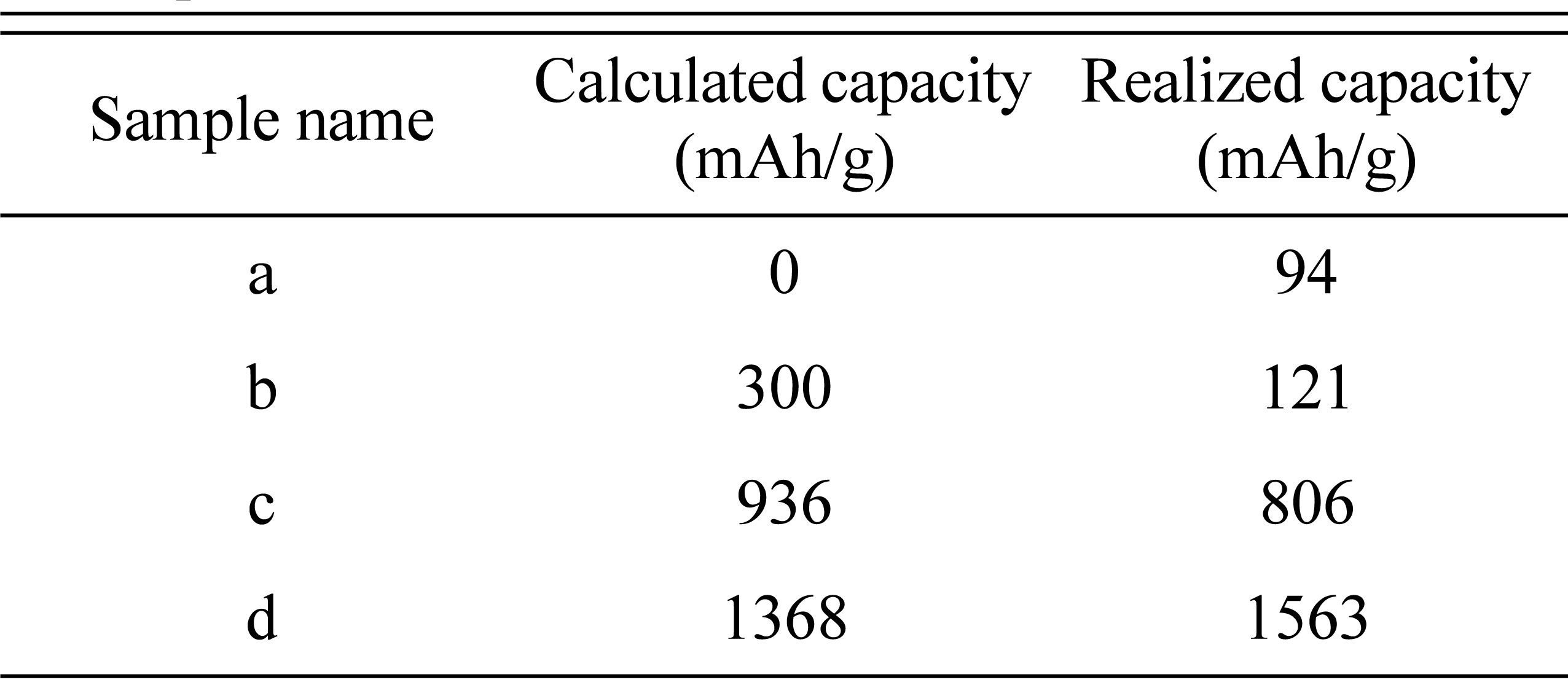
c by the lever rule of the phase diagram. The capacity estimation for all samples by the lever rule is summarized in
Table. 2.
Fig.┬Ā3.
Capacity estimation line (red) of samples b (a) and c (b) by the lever rule using the equilibrium phase diagram of the SiŌĆōFeŌĆōAl alloys at 600Ōäā.
Table┬Ā2.
Summary of the calculated capacities of the designed samples.

Fig. 4 and
Fig. 5 show the XRD patterns and STEM observations of the ribbon samples, respectively. In sample
a, as we expected, no XRD peaks of elemental Si (
Fig. 4(a)) were detected, indicating that all Si was transformed to the FeSi and FeSi
2 phases. Accordingly, no active Si grain was observed in the elemental mapping of Si, Al, and Fe as shown in
Fig. 5(a). The dark area coincides with the Fe-rich region and therefore is assumed to be FeSi. Meanwhile, the bright area is the FeSi
2 phase. Furthermore, SAED indexing confirmed our observations. Although we expected Al
2Fe
3Si
3 from the phase diagram, the corresponding peaks were not detected by XRD, probably, because of the low amount of Al in the alloy. The XRD indexing of sample
b revealed the FeSi
2 and Al
6Fe
4Si
6 phases (
Fig. 4(b)). In addition, from EDS mapping (
Fig.5 (b)), insignificant amounts of elemental Si (dark area) and Al grains (grey area) surrounded by FeSi
2 (bright area) were observed, which is in good agreement with our expected phases based on the phase diagram. Similarly, in sample
c, from XRD patterns (
Fig. 4(c)), we could identify the expected secondary phases along with crystalline Si.
Fig. 5(c) represents the clear separation between active Si with a grain size of about 200 nm and the matrix through elemental mapping. In sample
d, based on the XRD and TEM-EDS data analyses (
Figs. 4(d) and
5(d)), the homogeneous distribution of nanosized Si in a surrounded matrix consisting of the Al
6Fe
4Si
6 and Al
2FeSi ternary phases can be seen. The selected area electron diffraction results show the formation of polycrystalline Si and the matrix phases in all samples. Summary of the estimated and revealed phases is represented in
Table 3.
Fig.┬Ā4.
XRD patterns of samples a, b, c, and d.

Fig.┬Ā5.
STEMŌĆōEDS mapping of Si, Fe, and Al and SAED pattern of samples a, b, c, and d.

Table┬Ā3.
Summary of the expected and revealed phases.

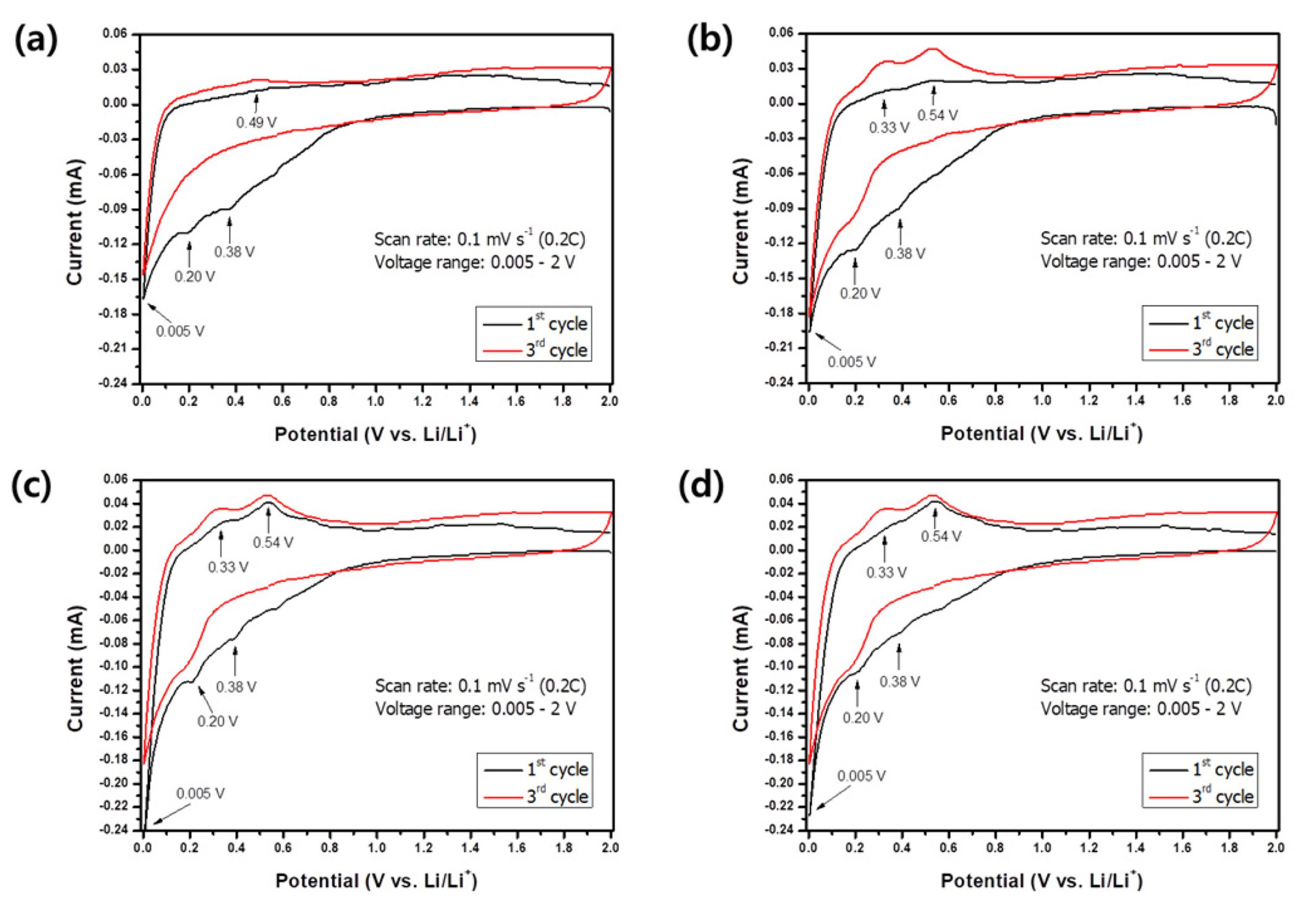
Fig. 6 shows typical CV curves of the Si alloys in the range of 0.005ŌĆō2 V at 0.1 mV/s (corresponds to 0.2 C). In the first lithiation, three reduction peaks appeared at 0.38, 0.2, and 0.005 V, respectively. The broad and indistinct peak at 0.38 V was observed only in the first lithiation and disappeared in the subsequent cycles. This indicates an irreversible reaction and was widely reported
[20-
22] as being attributed to the formation of a solid electrolyte interphase on the working electrode surface. Other reduction (at 0.2 V and 0.005 V) and oxidation (at 0.33 V and 0.54 V) peaks show good reversibility and are represented by Si phase changes upon the lithiation/delithiation process. Samples
b,
c, and
d show identical redox peaks; however, sample
a shows the oxidation peak at 0.5 V, which probably corresponds to the insignificant reactivity of other phases as reported elsewhere
[23].
Fig.┬Ā6.
Cyclic voltammograms of samples a, b, c, and d at a scan rate of 0.1 mV/s.
The charge/discharge curves of samples
a,
b,
c, and
d at a current density of 100 mA/g were examined during 30 cycles as illustrated in
Figs. 7(a),
7(c),
7(e), and
7(g), respectively. Samples
a and
b show reversible capacity <130 mAh/g. While, samples
c and
d show the initial discharge capacities of 806 and 1563 mAh/ g, respectively. Thus, these results are consistent with the proposed capacity estimation by the lever rule method. In samples
b,
c, and
d we found a discrepancy between the initial and 30
th cycles. The corresponding dQ/dV plots (
Figs. 7(d),
7(f), and
7(h)) clearly show the formation of the second oxidation peak at 0.3 V upon 30 cycles. Similar behavior was observed in our previous research on rapidly solidified SiŌĆōNi alloys
[24].
Fig.┬Ā7.
(a, c, e, g) ChargeŌĆōdischarge curves and (b, d, f, and h) dQ/dV plots of samples a, b, c, and d at a current density of 0.1 A/g.
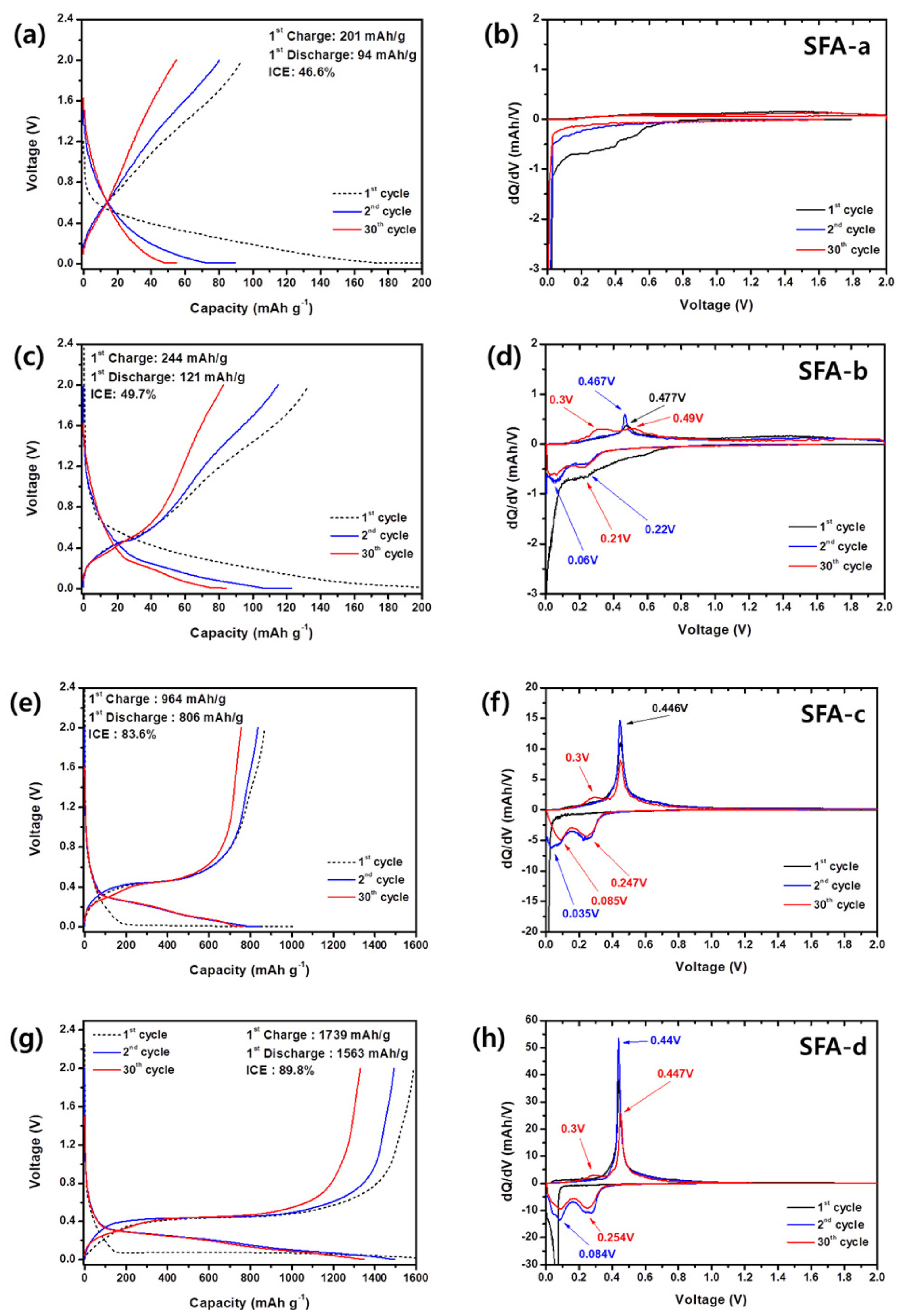
Fig. 8 depicts the cycle performance and the coulombic efficiency of various SiŌĆōFeŌĆōAl alloys over 30 cycles. All samples exhibit a high coulombic efficiency of >98%; however, in terms of the Li-ion battery application, the most attractive energy content was evaluated in samples
c and
d. Despite the highest initial discharge capacity in sample
d, the capacity retention gradually decreases compared to that of sample
c. Excellent cycle performance of sample
c can be explained by the lower amount of active Si in the matrix, and therefore less stress and strain occurred upon the reversible reaction with Li.
Fig.┬Ā8.
(a) Cycle performance and (b) Coulombic efficiency of samples a, b, c, and d at a current density of 0.1 A/g.
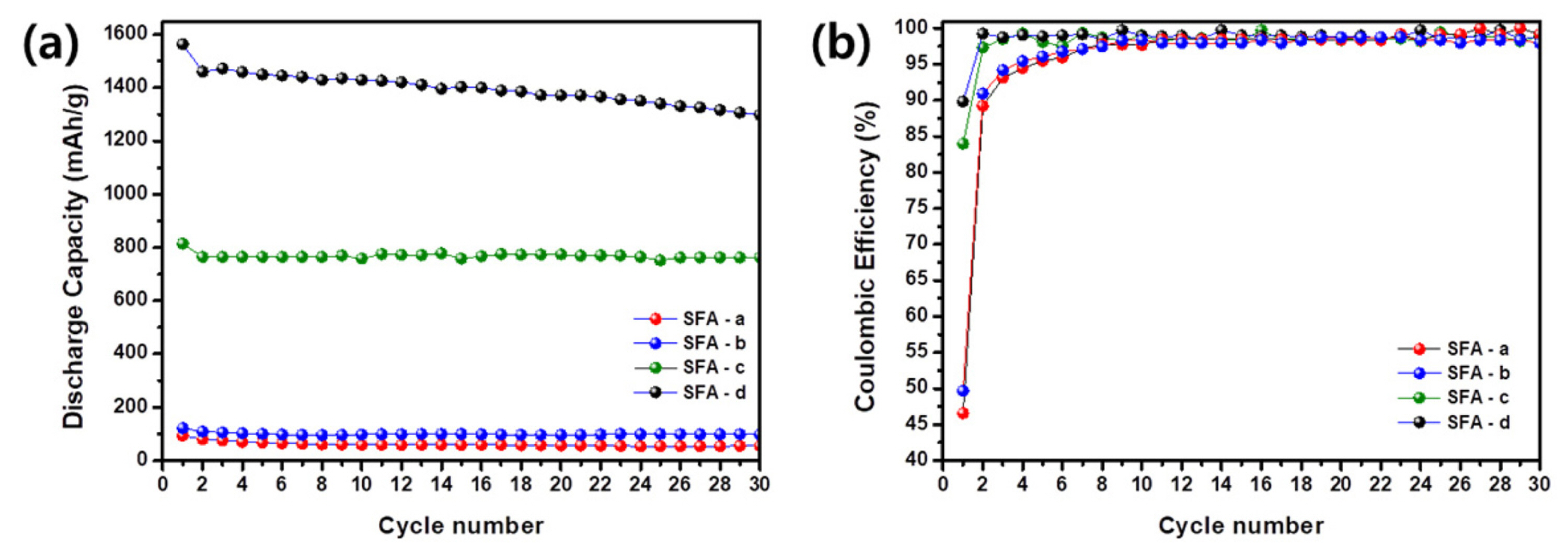
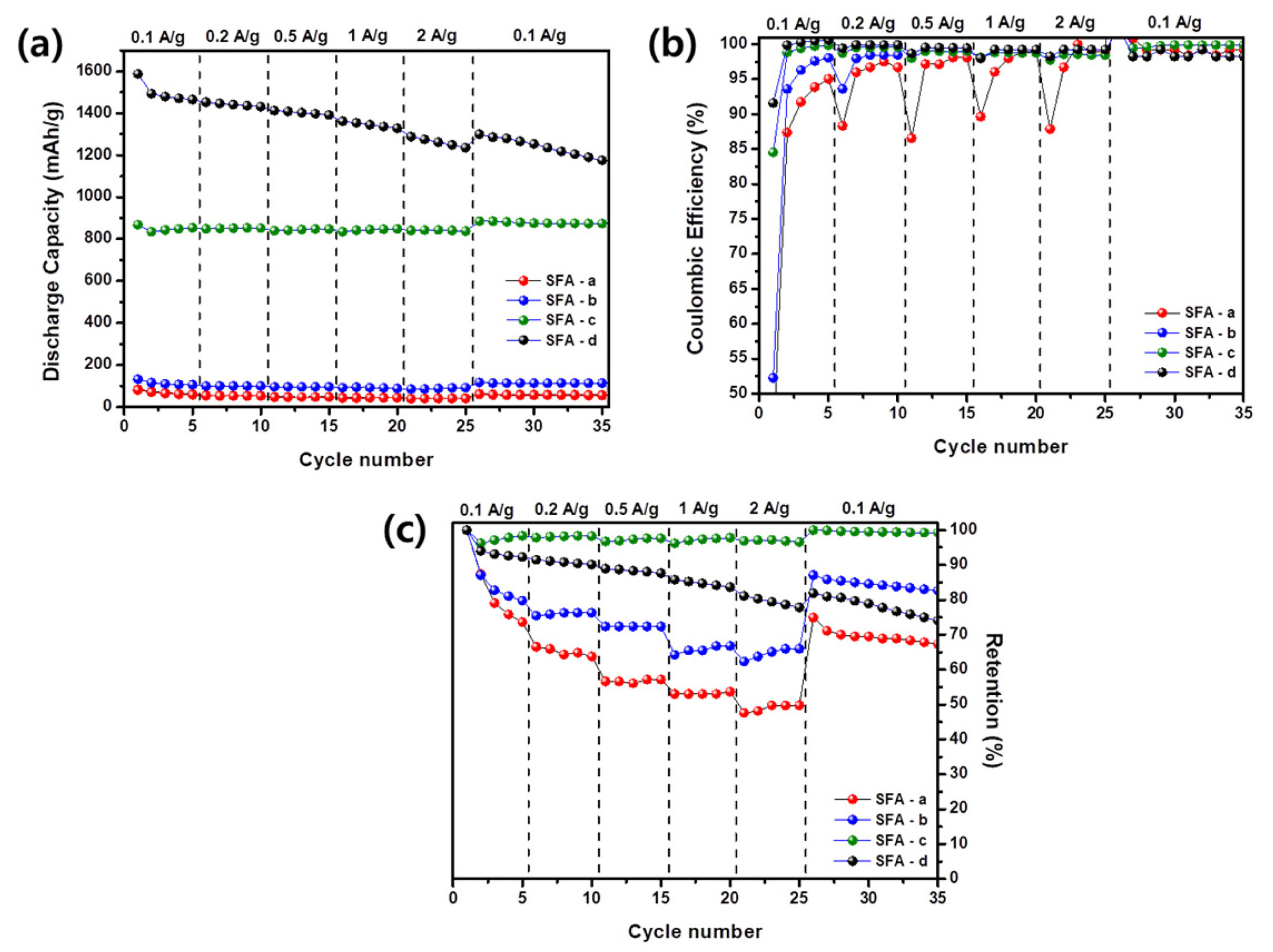
Fig. 9 shows the rate capability of samples
a,
b,
c, and
d evaluated at various current densities from 0.1 A/g to 2 A/g with an increment of five cycles. Here-inafter, the capacity recovery ability was evaluated at an initial current density of 0.1 A/g over ten cycles. Similarly as discussed above, the samples
a,
b and
d shows steady capacity fading upon cycling under high current densities. An extraordinary rate capability over high current densities was revealed in sample
c. Indeed, such durability was achieved owing to intrinsic properties of the matrix to accommodate the volume expansion of Si along with the improved conductivity.
Fig.┬Ā9.
(a) Rate capability, (b) Coulombic efficiency, and (c) capacity retention of samples a, b, c, and d.
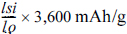 ) as shown in Fig. 3(a). The reversible reaction was assumed to be Li3.75Si with an identical capacity of about 3600 mAh/g [7, 14]. According to the same estimation procedure, the capacities of samples c and d were expected to be 963 mAh/g and 1368 mAh/g, respectively. Fig. 3(b) shows the capacity estimation of sample c by the lever rule of the phase diagram. The capacity estimation for all samples by the lever rule is summarized in Table. 2.
) as shown in Fig. 3(a). The reversible reaction was assumed to be Li3.75Si with an identical capacity of about 3600 mAh/g [7, 14]. According to the same estimation procedure, the capacities of samples c and d were expected to be 963 mAh/g and 1368 mAh/g, respectively. Fig. 3(b) shows the capacity estimation of sample c by the lever rule of the phase diagram. The capacity estimation for all samples by the lever rule is summarized in Table. 2.