Electrochemical Effectiveness Factors for Butler-Volmer Reaction Kinetics in Active Electrode Layers of Solid Oxide Fuel Cells
Article information
Abstract
In this study, a numerical approach is adopted to investigate the effectiveness factors for distributed electrochemical reactions in thin active reaction layers of solid oxide fuel cells (SOFCs), taking into account the Butler-Volmer reaction kinetics. The mathematical equations for the electrochemical reaction and charge conduction process were formulated by assuming that the active reaction layer has a small thickness, homogeneous microstructure, and high effective electronic conductivity. The effectiveness factor is defined as the ratio of the actual reaction rate (or equivalently, current generation rate) in the active reaction layer to the nominal reaction rate. From extensive numerical calculations, the effectiveness factors were obtained for various charge transfer coefficients of 0.3-0.8. These effectiveness data were then fitted to simple correlation equations, and the resulting correlation coefficients are presented along with estimated magnitude of error.
1. Introduction
Solid oxide fuel cells (SOFCs) are a promising high-temperature fuel cell technology that can efficiently convert the chemical energy of fuel into electricity [1, 2]. The high operating temperature (~800-1000℃) of SOFCs reduces manufacturing costs by employing non-precious metal catalyst, directly uses hydrocarbon fuels by utilizing internal reforming, and achieves higher overall efficiency through the construction of hybrid or combined heat and power (CHP) systems. However, the high operating temperature of SOFCs tends to accelerate the microstructural degradation of electrodes, thereby negatively affecting the long-term performance stability. Thus, intermediate-temperature SOFCs (IT-SOFCs) that can operate at ~650-800℃ have emerged as a solution to the long-term performance degradation problem [3-5].
To achieve better performance of IT-SOFCs, material scientists have focused on the development of new materials, such as electrolyte materials with higher ionic conductivities and electrode materials with higher electrochemical activities, at these intermediate temperature ranges [6-8]. Concurrently, other researchers have attempted to determine the optimal electrode structure that can maximize the electrode performance for a given material. For this purpose, multilayer [9-12], and functionally or microstructurally graded electrode structures [13-15] have been proposed to enhance the electrochemical performance of IT-SOFCs. In addition, recent experimental studies have directly reconstructed three-dimensional electrode microstructures using advanced imaging techniques, through which the relationship between the electrode microstructural parameters and electrochemical efficiencies has been investigated [16-18].
In multilayer electrodes of IT-SOFCs, a thin layer dedicated to the electrochemical reactions is in direct contact with the electrolyte. This layer is called the active reaction layer and is made by mixing fine electronic and ionic conductor particles, to provide rich three-phase boundaries (TPBs) for electrochemical reactions. In the exterior of the active reaction layer, a bulk transport layer is formed to facilitate fast mass transport and electron conduction. Almost all electrochemical reactions occur inside the active reaction layer, which highlights that microstructural optimization of the active reaction layer is essential for improved IT-SOFC performance. In this regard, the electrochemical effectiveness factor has been investigated as an appropriate measure for evaluating the efficiency of electrodes.
Previously, Costamagna et al. [19,20] proposed the electrochemical effectiveness concept in search of the optimal microstructure for SOFC electrodes. However, their model is based on the linear transfer current-local overpotential (i-η) relationship, and thus is valid only for very low current density (or equally, for very low overpotential) conditions. Recently, Shin and Nam [21] resolved this limitation by considering a nonlinear i-η relationship, the symmetric Butler-Volmer reaction kinetics. They showed that the electrochemical effectiveness factor can be decomposed into the base effectiveness at zero overpotential and the relative effectiveness at finite overpotentials. In addition, a simple correlation equation was also proposed along with the correlation coefficients relevant to the symmetric Butler-Volmer reaction kinetics. Their model was successfully used for one-dimensional simulation of a single-cell SOFC [22] and the theoretical prediction of electrode microstructural effects [23,24].
In this study, the work of Shin and Nam [21] is further extended by considering both the symmetric and asymmetric Butler-Volmer reaction kinetics. As before, the active reaction layer is assumed to be homogeneous in microstructure and sufficiently thin to ensure uniform conditions (temperature, pressure, and species concentration). In addition, the electronic potential is assumed to be uniform inside the reaction layer, since the effective electronic conductivity is much higher that the effective ionic conductivity. The effectiveness factors for current generation performance (or equally, electrochemical reaction efficiency) in the active reaction layer were numerically obtained by varying the charge transfer coefficient from 0.3 to 0.8. Finally, the calculated effectiveness data were fitted to the correlation equation proposed by Shin and Nam [21], from which the correlation coefficients and estimated errors were determined.
2. Theory and Calculations
2.1 Physical model and assumptions
The fuel cell processes inside the two-layer anode of IT-SOFCs are illustrated in Fig. 1, where the species transport, charge conduction, and distributed electrochemical reactions are indicated. The active reaction layer in the anode is very thin (~20 μm) and is composed of fine electronic (Ni) and ionic (YSZ; yttriastabilized zirconia) conductor particles (whose mean particle diameter is ~0.5 μm) to provide rich TPB sites for electrochemical reactions. In contrast, the bulk transport layer in the anode is relatively thick and is made of coarse particles to enable fast mass transport (also to provide structural support in the case of anode-supported IT-SOFCs). In Fig. 1, the electronic current, Iel, ionic current, Iio, and charge transfer current, Itr, are also illustrated to explain the distributed nature of electrochemical reactions in the active reaction layer. In the anode, the electronic current, Iel, decreases in magnitude as it flows towards the electrolyte in direct proportion to the charge transfer current, Itr (or equally, the electrochemical reaction rate). Accordingly, the ionic current, Iio, increases in magnitude by collecting Itr, and flows through the electrolyte and towards the cathode.

Electrochemical reactions and transport processes (mass diffusion and charge conduction) in the two-layer anode of IT-SOFCs, along with the resultant electronic current, Iel, ionic current, Iio, and charge transfer current, Itr.
The conservation of electron, oxygen ion, and gas species, along with the electrochemical reactions, should be considered in the simulation of fuel cell processes in the active reaction layer. In this study, it is assumed that the active reaction layer is homogeneous in microstructure, sufficiently thin to ensure uniform operating condition (temperature, pressure, and species concentration), and has a significantly higher effective electronic conductivity, σel,eff, compared to its effective ionic conductivity, σio,eff. These are believed to be practical assumptions that lead to negligible errors in the results [21,22]. The physical interpretation of each assumption can be summarized as follows.
• Homogeneous microstructure: The volume-specific TPB length (TPBL), λtpb,V, and the effective ionic conductivity, σio,eff, are uniform inside the active reaction layer.
• Uniform operating condition: The TPBL-specific exchange current density, itpb, is uniform inside the active reaction layer. In addition, the Nernst potential, φo , and the concentration overpotential, ηconc, are also uniform.
• High effective electronic conductivity: The electronic potential, φel, is relatively uniform inside the active reaction layer, compared with the variation of the ionic potential, φio.
2.2 Governing equations and reaction kinetics
The governing equations and boundary conditions for electronic and ionic charge conservation can be expressed for the active reaction layer in the anode of IT-SOFCs (shown in Fig. 1) as [20,21]

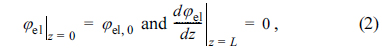

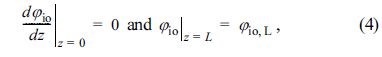
where iel is the electronic current density, iio is the ionic current density, and itr,V(η) is the volumetric charge transfer current density at the local activation overpotential of η. In addition, φel,0 denotes the electronic potential at z = 0 and φio,L denotes the ionic potential at z = 0.
In this study, φel is assumed to be uniform inside the active reaction layer, such that φel(z) = φel,0; thus, it is not necessary to solve Eqs. (1) and (2). It should be noted that the local activation overpotential, η, is defined as
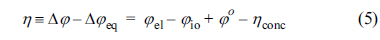
where φo is the Nernst potential and ηconc is the concentration overpotential. In Eq. (5), φel, φo, and ηconc are all constant inside the active reaction layer according to the assumptions of this study. Then, the governing equations and boundary conditions for ionic charge conservation, Eqs. (3) and (4), can be expressed in terms of η as
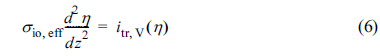

Here, ηconc is the total activation overpotential applied on the active reaction layer, determined as

Eq. (6) can be alternatively obtained by subtracting Eq. (3) from Eq. (1), based on the relation ▽2η = ▽2φel – ▽2φio [20]. In this case, σio,eff in Eq. (6) should be replaced with the effective charge conductivity, σeff, defined as σeff = (1/σio,eff + 1/σel,eff)-1. When σel,eff is much larger than σio,eff, as considered in this study, σeff is approximately equal to σio,eff. It should be noted that Eqs. (6) and (7) are valid for both the anode and cathode reaction layers.
According to the Butler-Volmer equation, the volumetric charge transfer current density, itr,V(η), is expressed as

where α is the charge transfer coefficient, ne is the number of electrons (2 for the anodic reaction and 4 for the cathodic reaction), F is the Faraday constant (96,485 C mol-1), R is the universal gas constant (8.314 J mol-1 K-1), and T is the temperature in Kelvin. In Eq. (9), the volumetric exchange current density, iex,V, can be obtained by multiplying the TPBL-specific exchange current density, itpb, and the volume-specific TPBL, λtpb,V as iex,V = itpb × λtpb,V. Note that Eq. (9) may also be expressed in terms of the TPBL-specific polarization resistance, rtpb (Ωm), as

Fig. 2 shows the charge transfer current density vs. local activation overpotential (itr,V-η) curves for the Butler-Volmer reaction kinetics (ne = 2 and T = 1000 K are assumed) determined using Eqs. (9) and (10). A larger charge transfer coefficient, α, leads to a smaller activation overpotential for a given transfer current density. As shown in Fig. 2, the Butler-Volmer equation is reduced to a single linear polarization equation at very small overpotentials, irrespective of the charge transfer coefficient. The asymptotic expansion of Eqs. (9) and (10) results in
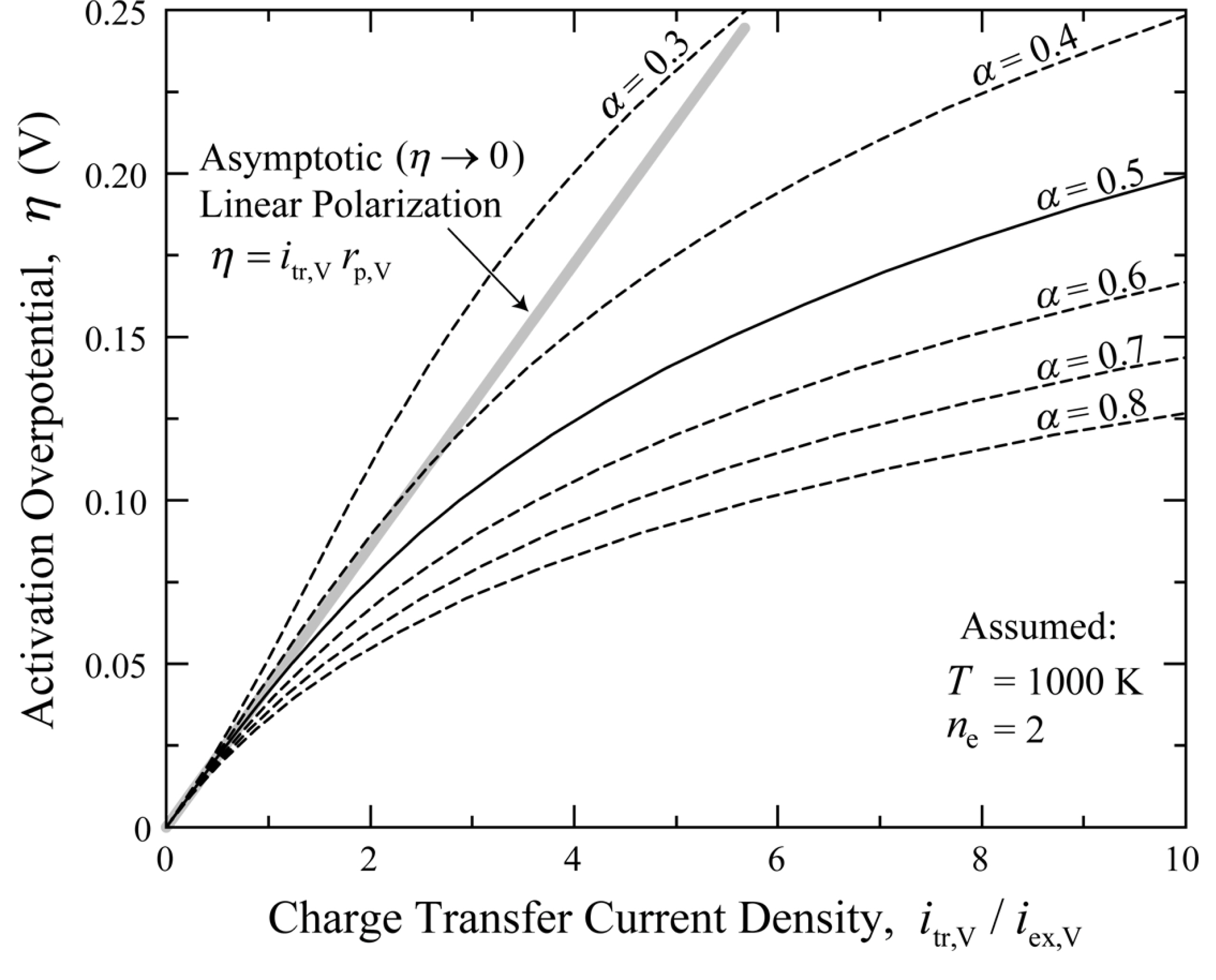
Charge transfer current density vs. local activation overpotential (itr,V-η) curves for general Butler-Volmer reaction kinetics of Eq. (9) with various charge transfer coefficients. These curves are obtained for anodic reaction (ne = 2) at T = 1000 K.
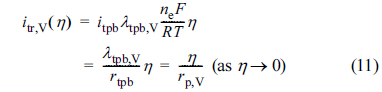
where rp,V is the volume-specific linear polarization resistance (rp,V = rtpb / λtpb,V).
The charge transfer coefficient is an indicator of the symmetry of the activation energy barrier when a positive or negative overpotential is applied [25]. In SOFC modeling studies, the coefficient is generally assumed to be 0.5 (symmetric Butler-Volmer equation), primarily due to the lack of experimental data [26]. However, detailed electrochemical kinetic studies [26-29] on Ni pattern anodes or Ni cermet anodes has shown that the charge transfer coefficient can have values different from 0.5. For example, the charge transfer coefficient, α, for hydrogen oxidation on Ni/YSZ anodes was estimated to be 0.6-0.7 by Utz et al. [26] and approximately 0.7 by Holtappels et al. [29]. Thus, the development of the general electrochemical effectiveness model for both the symmetric and asymmetric Butler-Volmer reaction kinetics is important.
2.3 Effectiveness model and correlations
The effectiveness factor, Γeff, has been defined as the ratio of the actual current generation rate (or equally, the electrochemical reaction rate) in the active reaction layer to the maximum current generation rate as [20,21]
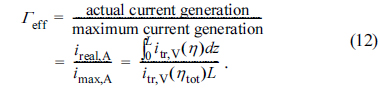
In Eq. (12), the actual current density, ireal,A, is calculated by integrating itr,V(η) in the active reaction layer (0 ≤ z ≤ L), while the maximum current density, imax,A, is directly obtained by multiplying itr,V(ηtot) and the layer thickness, L. Note that the maximum current density is obtained when all the TPB sites inside the active reaction layer are uniformly subject to ηtot. In real situations, the local overpotential, η, is usually smaller than ηtot (η ≤ ηtot) inside the reaction layer and thus the effectiveness factor, Γeff, is always equal to or smaller than 1 (0 ≤ Γeff ≤ 1).
It was shown by Costamagna et al. [20] that the effectiveness factor for a linear charge transfer reaction, such as Eq. (11), can be expressed as

where ϕT is the electrochemical Thiele modulus, defined as
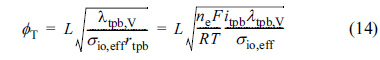
Note that Γeff in Eq. (13) has the same functional form as the effectiveness factor for chemical reaction/mass transfer in heterogeneous catalysis, or the fin efficiency for conduction/convection heat transfer in extended surfaces (fins). The Thiele modulus, ϕT, usually has a value in the range of 5-20 for the anode reaction layers and 0.5-2.0 for the cathode reaction layers, for ordinary operation of IT-SOFCs [21,22].
Shin and Nam [21] studied the effectiveness factor for the symmetric Butler-Volmer reaction kinetics, such as Eqs. (9) and (10) with α = 0.5. From extensive numerical calculations, they showed that the effectiveness factor, Γeff, for nonlinear reaction kinetics can be decomposed into two parts, namely, the base effectiveness at zero activation overpotential, Γeff,0V, and the relative effectiveness at finite activation overpotential,  , as
, as
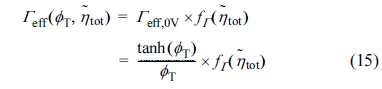
Here, 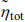 is the dimensionless total activation over-potential applied on the active reaction layer
is the dimensionless total activation over-potential applied on the active reaction layer  . In Eq. (15),
. In Eq. (15), 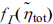 depends on
depends on 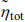 , not separately on α, ne, T or ηtot. It is also shown that
, not separately on α, ne, T or ηtot. It is also shown that 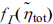 has a nearly constant functional form with respect to
has a nearly constant functional form with respect to 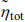 for ϕT ≥ 3.
for ϕT ≥ 3.
It is not convenient to present all the effectiveness factors for various ϕT and 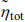 in a tabulated form because of their large data size. Thus, Shin and Nam [21] proposed a simple correlation equation for easy and accurate determination of the electrochemical effectiveness data, which is written as
in a tabulated form because of their large data size. Thus, Shin and Nam [21] proposed a simple correlation equation for easy and accurate determination of the electrochemical effectiveness data, which is written as

where a, b, c, and d are the correlation coefficients dependent on ϕT. Eq. (16) accurately describes the behavior of the relative effectiveness, 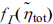 , starting from 1.0 at a very small ϕT, and decreasing towards 0.0 as ϕT increases.
, starting from 1.0 at a very small ϕT, and decreasing towards 0.0 as ϕT increases.
Using the electrochemical effectiveness factor, the current generation in the active reaction layer can be determined according to the following steps. First, the TPBL-specific exchange current density, itpb, or the TPBL-specific linear polarization resistance, rtpb, is calculated for given operating conditions. Second, the electrochemical Thiele modulus, ϕT, is calculated using Eq. (14). Third, the base effectiveness, Γeff,0V, and the relative effectiveness, 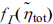 , are calculated using Eqs. (15) and (16), from which the electrochemical effectiveness factor, Γeff, is determined. Once Γeff is known, the actual current density, ireal,A, generated in the active reaction layer is obtained as
, are calculated using Eqs. (15) and (16), from which the electrochemical effectiveness factor, Γeff, is determined. Once Γeff is known, the actual current density, ireal,A, generated in the active reaction layer is obtained as
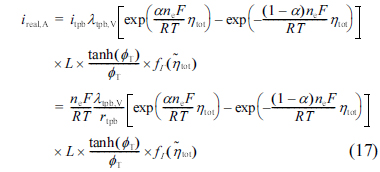
2.4 Numerical calculations
The governing equations and boundary conditions provided in Eqs. (6), (7), and (10) were discretized using the finite difference method (FDM). Uniform 2000 grid points were placed in the one-dimensional calculation domain of the active reaction layer (0 ≤ z ≤ L). The discretized nonlinear algebraic equations were solved using the Engineering Equation Solver (EES) software [30]. Once the converged solution is obtained, the effectiveness factor was decomposed into the base effectiveness, Γeff,0V, and the relative effectiveness, 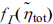 . In this study, numerical calculations were performed for both the symmetric and asymmetric Butler-Volmer reaction kinetics, by varying the charge transfer coefficient, α, as 0.3, 0.4, 0.5, 0.6, 0.7, and 0.8.
. In this study, numerical calculations were performed for both the symmetric and asymmetric Butler-Volmer reaction kinetics, by varying the charge transfer coefficient, α, as 0.3, 0.4, 0.5, 0.6, 0.7, and 0.8.
3. Results and Discussion
3.1 Symmetric Butler-Volmer reaction kinetics
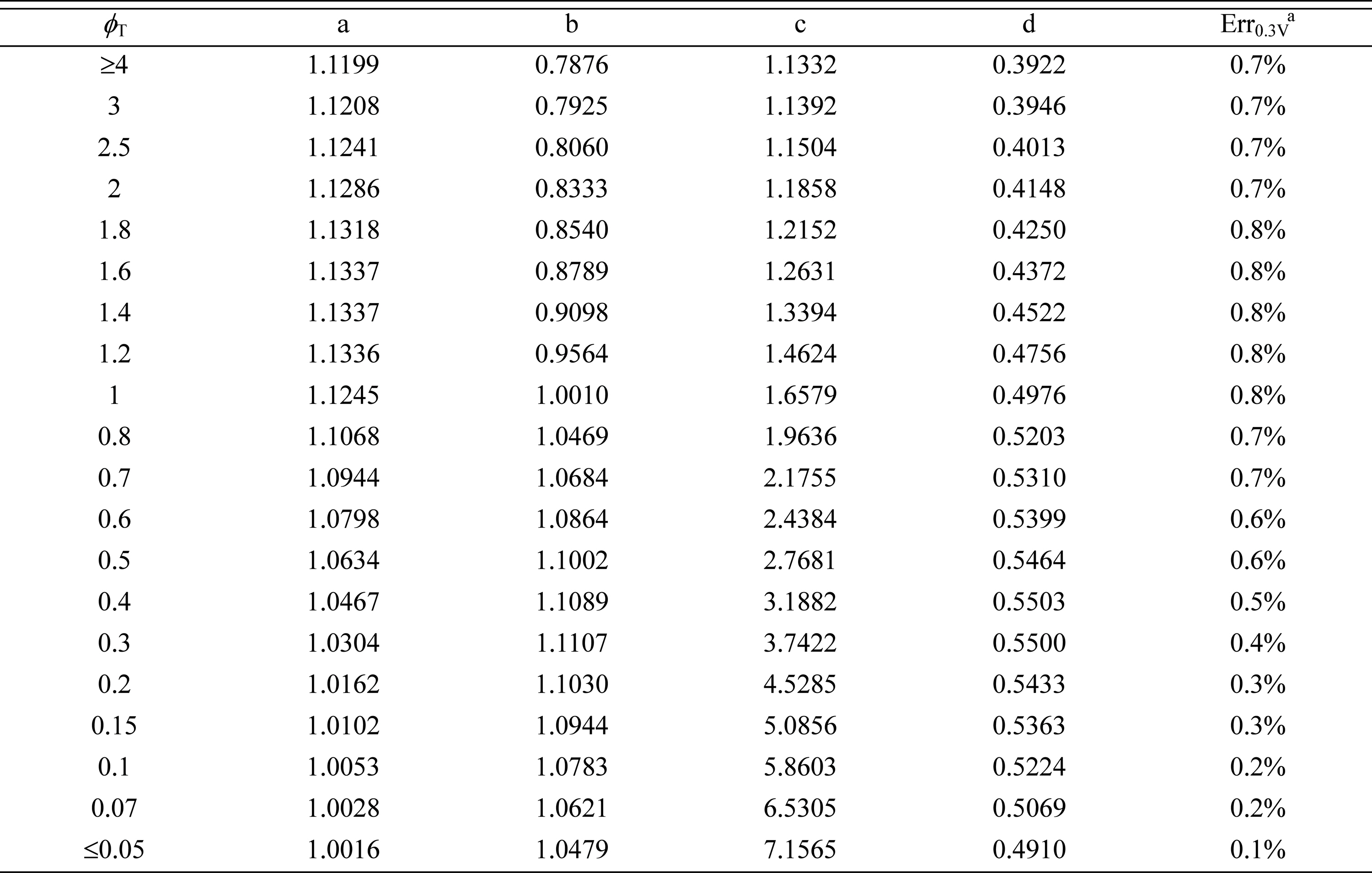
Previously, Shin and Nam [21] investigated the electrochemical effectiveness factors for current generation in the active reaction layers, subject to the symmetric Butler-Volmer reaction kinetics (α = 0.5). The results and the accuracy of the electrochemical effectiveness model are briefly reviewed in this section.
Fig. 3 presents the relative effectiveness factor, 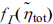 , which was numerically determined by solving Eqs. (6), (7), and (10) with α = 0.5 (symmetric Butler-Volmer equation). In Fig. 3,
, which was numerically determined by solving Eqs. (6), (7), and (10) with α = 0.5 (symmetric Butler-Volmer equation). In Fig. 3, 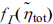 generally decreases from 1.0 towards 0.0 as increases. For a given
generally decreases from 1.0 towards 0.0 as increases. For a given 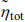 ,
, 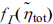 becomes smaller as ϕT increases. It is interesting to note that
becomes smaller as ϕT increases. It is interesting to note that 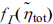 seems to have a constant functional shape when ϕT is higher than 3 (ϕT ≥ 3). Shin and Nam [21] showed that this behavior occurs when the active reaction layer thickness, L, becomes sufficiently thick, such that further increase of L does not contribute to the enhancement of current generation.
seems to have a constant functional shape when ϕT is higher than 3 (ϕT ≥ 3). Shin and Nam [21] showed that this behavior occurs when the active reaction layer thickness, L, becomes sufficiently thick, such that further increase of L does not contribute to the enhancement of current generation.
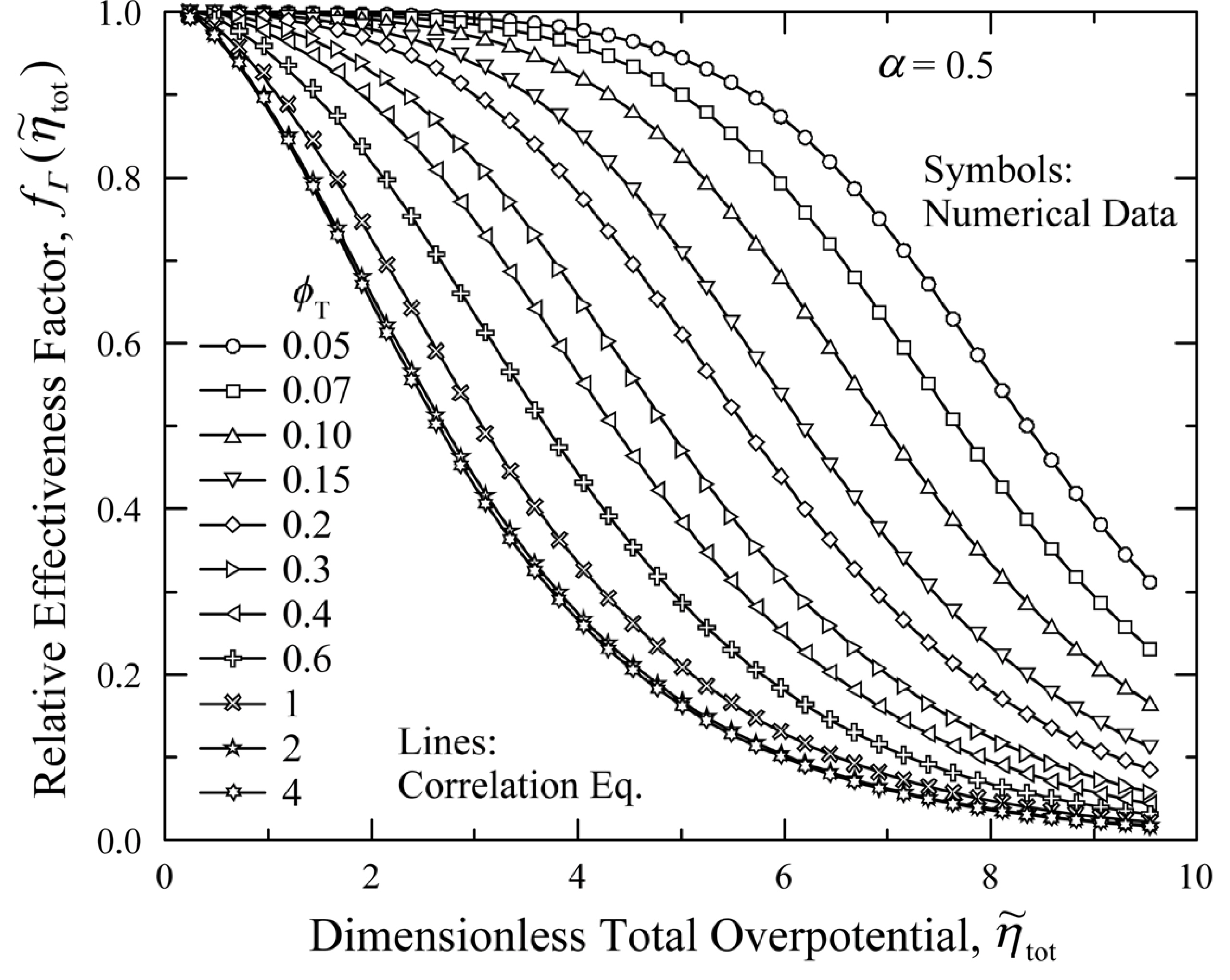
Relative effectiveness factor,  , for the current generation performance of the active reaction layer in IT-SOFCs: Symmetric Butler-Volmer reaction kinetics with α = 0.5.
, for the current generation performance of the active reaction layer in IT-SOFCs: Symmetric Butler-Volmer reaction kinetics with α = 0.5.
In Fig. 3, “symbols” denote the relative effectiveness data obtained by numerical calculation, while “lines” denote the curves that are fitted to the correlation equation of Eq. (16). The correlation coefficients, a, b, c, and d, are listed in Table 1, along with the estimated errors. The results clearly indicate that using Eq. (16) for estimating 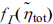 results in a small error (less than 1%). Thus, Eq. (16) and Table 1 can be viewed as a complete solution for the electrochemical effectiveness for symmetric Butler-Volmer reaction kinetics, described by Eqs. (6), (7), and (10).
results in a small error (less than 1%). Thus, Eq. (16) and Table 1 can be viewed as a complete solution for the electrochemical effectiveness for symmetric Butler-Volmer reaction kinetics, described by Eqs. (6), (7), and (10).
The accuracy of the electrochemical effectiveness factors provided in Fig. 3 and Table 1 was fully validated by Shin and Nam [21]. Excellent agreement was observed between the current-overpotential performance curves obtained by the effectiveness model and those obtained by the detailed electrode microscale model. In addition, a one-dimensional simulation model was also developed to predict the current-voltage performance curves of a single-cell SOFC with two-layer electrodes (anode and cathode) [22]. The results obtained were essentially the same as the more detailed comprehensive microscale model results [12]. Thus, the electrochemical effectiveness factors presented in this study enable efficient calculation of the current density in the anode and cathode functional layers of SOFCs, without addressing the detailed electrochemical reaction/charge transport processes therein.
3.2 Asymmetric ButlerVolmer reaction kinetics with α > 0.5
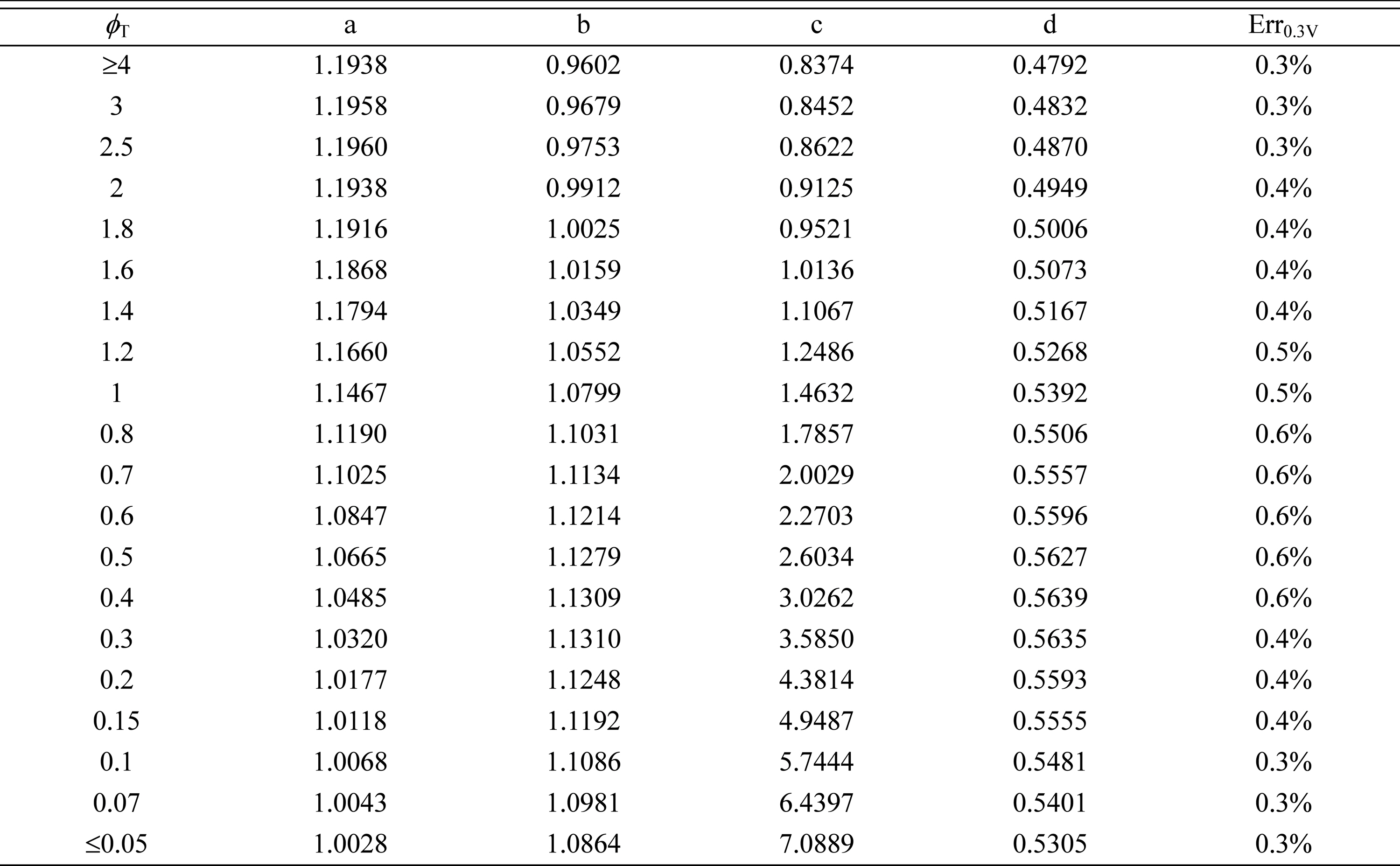
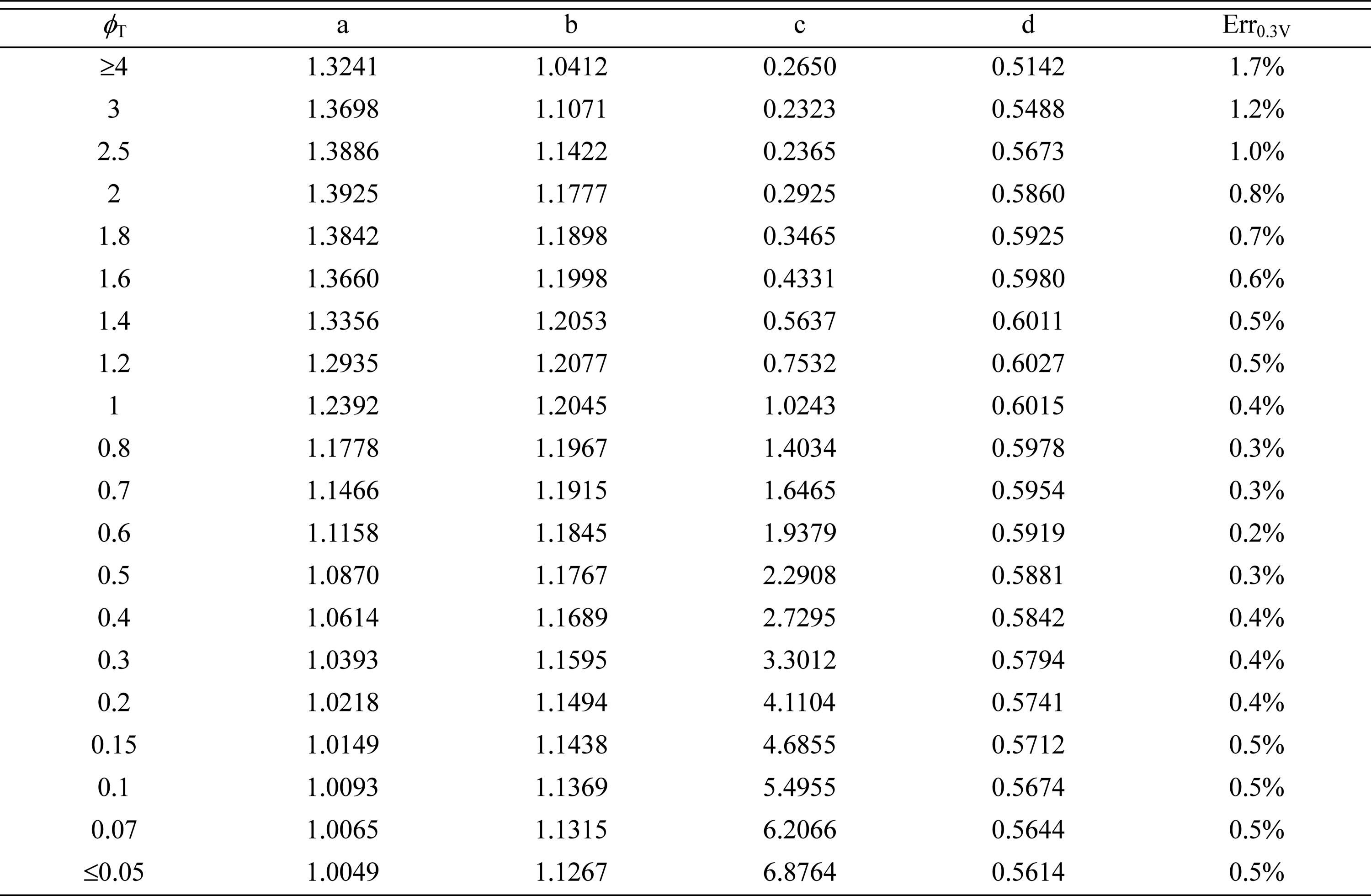
To extend the work of Shin and Nam [21], extensive numerical calculations were performed to determine the effectiveness factors for current generation subject to asymmetric Butler-Volmer reaction kinetics with α > 0.5 (see Fig. 2). Fig. 4 show the relative effectiveness data (symbols) and correlation equations (lines) for α = 0.6, 0.7, and 0.8. The general behavior of  for α > 0.5 shown in Fig. 4 is similar to the behavior for α = 0.5 shown in Fig. 3, except that the range of
for α > 0.5 shown in Fig. 4 is similar to the behavior for α = 0.5 shown in Fig. 3, except that the range of 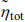 increases with α according to
increases with α according to 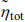 = αneFηtot / RT. The correlation coefficients are provided in Tables 2, 3, and 4. These tables summarize the maximum correlation errors encountered for the cathode total over-potential in the range of 0-0.3 V (equivalently, the anode total overpotential range of 0-0.6 V) at T = 1000 K.
= αneFηtot / RT. The correlation coefficients are provided in Tables 2, 3, and 4. These tables summarize the maximum correlation errors encountered for the cathode total over-potential in the range of 0-0.3 V (equivalently, the anode total overpotential range of 0-0.6 V) at T = 1000 K.

Relative effectiveness factor,  , for the current generation performance of the active reaction layer in IT-SOFCs: Asymmetric Butler-Volmer reaction kinetics with (a) α = 0.6, (b) α = 0.7, and (c) α = 0.8.
, for the current generation performance of the active reaction layer in IT-SOFCs: Asymmetric Butler-Volmer reaction kinetics with (a) α = 0.6, (b) α = 0.7, and (c) α = 0.8.
Relatively good agreement between the numerical effectiveness data denoted by “symbols” and the correlation equations denoted by “lines” is observed in Fig. 4. In Tables 2-4, the maximum correlation error, Err0.3V, for the cathode total overpotential in the range of 0-0.3 V at T = 1000 K, is smaller than 0.6% for α = 0.6, smaller than 0.5% for α = 0.7, and smaller than 1.7% for α = 0.8. This result indicates that the proposed correlation equation of Eq. (16) accurately describes the behavior of 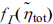 relevant to asymmetric Butler-Volmer reaction kinetics with 0.5 < α ≤ 0.8.
relevant to asymmetric Butler-Volmer reaction kinetics with 0.5 < α ≤ 0.8.
3.3 Asymmetric ButlerVolmer reaction kinetics with α < 0.5
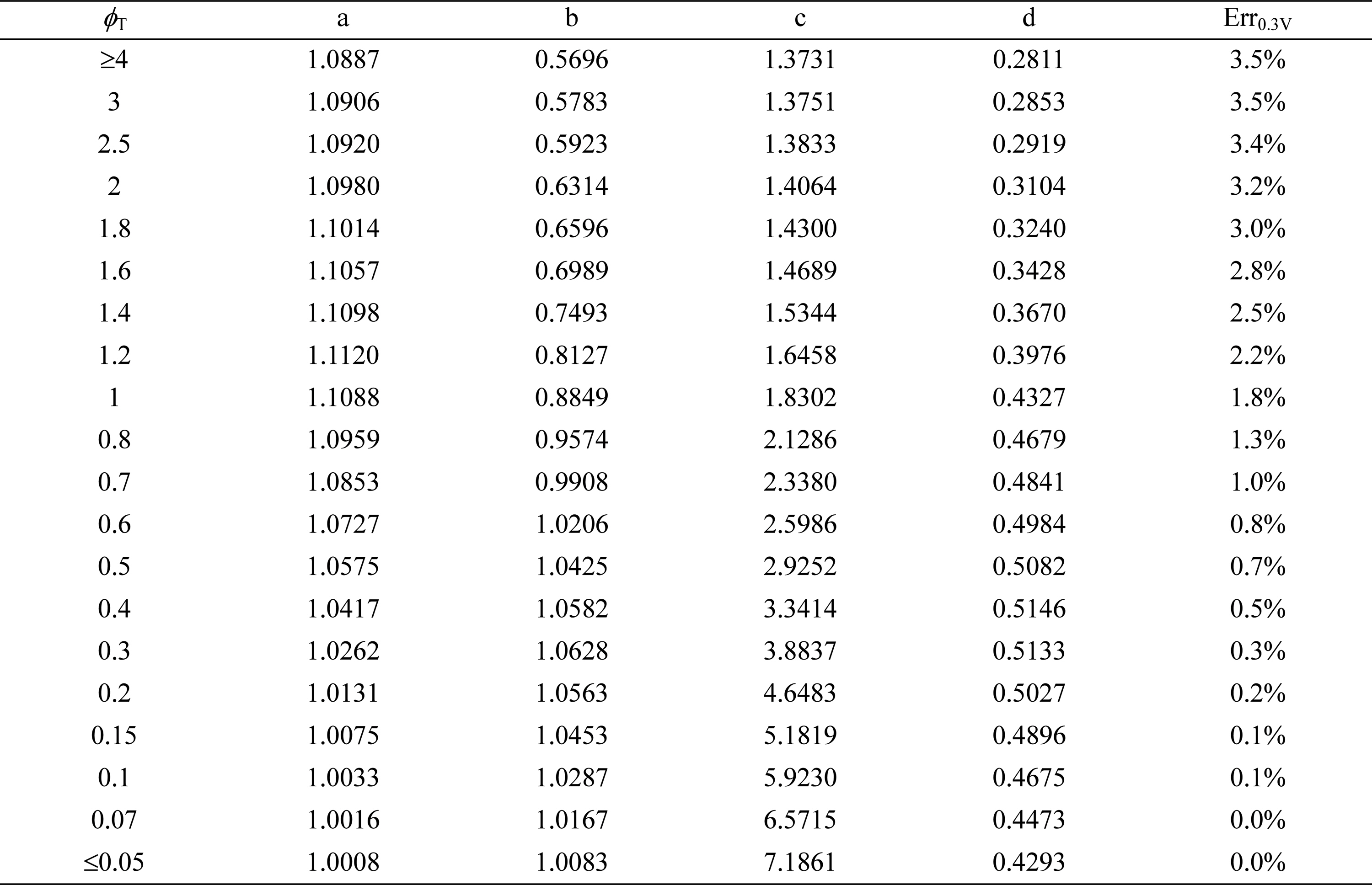
Numerical calculations were also conducted to determine the electrochemical effectiveness for electrochemical reactions in the thin active reaction layers when subject to asymmetric Butler-Volmer reaction kinetics with α < 0.5 (see Fig. 2). Figs. 5(a) and 5(b) show the relative effectiveness data (symbols) and correlation equations (lines) for α = 0.4 and 0.3, respectively, while the correlation coefficients are provided in Tables 5 and 6.
Relative effectiveness factor,  , for the current generation performance of the active reaction layer in IT-SOFCs: Asymmetric Butler-Volmer reaction kinetics with (a) α = 0.4 and (b) α = 0.3.
, for the current generation performance of the active reaction layer in IT-SOFCs: Asymmetric Butler-Volmer reaction kinetics with (a) α = 0.4 and (b) α = 0.3.
Fig. 5 shows that the relative effectiveness,  , has values higher than 1.0 for small
, has values higher than 1.0 for small  ranges, which is different from the behavior of
ranges, which is different from the behavior of 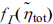 for symmetric (α = 0.5) and asymmetric (α > 0.5) Butler-Volmer reaction kinetics shown in Figs. 3 and 4, respectively. This trend can be explained by the ButlerVolmer reaction kinetics curves shown in Fig. 2. The Butler-Volmer equation with α ≥ 0.5 always results in a higher transfer current density at a given overpotential, compared with the linear polarization equation. The relative effectiveness,
for symmetric (α = 0.5) and asymmetric (α > 0.5) Butler-Volmer reaction kinetics shown in Figs. 3 and 4, respectively. This trend can be explained by the ButlerVolmer reaction kinetics curves shown in Fig. 2. The Butler-Volmer equation with α ≥ 0.5 always results in a higher transfer current density at a given overpotential, compared with the linear polarization equation. The relative effectiveness, 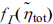 , is equal to 1.0 when the transfer current density vs. local activation overpotential (itr,V-η) curve strictly follows the linear polarization relationship. The deviation of itr,V-η curves with α ≥ 0.5 from the linear polarization relationship leads to
, is equal to 1.0 when the transfer current density vs. local activation overpotential (itr,V-η) curve strictly follows the linear polarization relationship. The deviation of itr,V-η curves with α ≥ 0.5 from the linear polarization relationship leads to 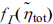 which is smaller than 1.0 in Figs. 3 and 4. In contrast, the Butler-Volmer equation with α < 0.5 has a low overpotential region where the transfer current density is smaller than the linear polarization relationship (for η in the range of 0-0.12 V with α = 0.4 and for η in the range of 0-0.26 V with α = 0.3 in Fig. 2). Thus, the relative effectiveness,
which is smaller than 1.0 in Figs. 3 and 4. In contrast, the Butler-Volmer equation with α < 0.5 has a low overpotential region where the transfer current density is smaller than the linear polarization relationship (for η in the range of 0-0.12 V with α = 0.4 and for η in the range of 0-0.26 V with α = 0.3 in Fig. 2). Thus, the relative effectiveness, 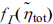 , becomes larger than 1.0 in those low overpotential regions (for
, becomes larger than 1.0 in those low overpotential regions (for 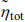 in the range of 0-1.1 with α = 0.4 and for
in the range of 0-1.1 with α = 0.4 and for 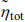 in the range of 0-1.8 with α = 0.3 in Fig. 5).
in the range of 0-1.8 with α = 0.3 in Fig. 5).
In this study, the correlation equation of Eq. (16) was replaced with the following equation for α < 0.5 to describe the observed behavior of 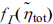 greater than 1.0. The lines in Fig. 5 represent the fitting curves of Eq. (18).
greater than 1.0. The lines in Fig. 5 represent the fitting curves of Eq. (18).

In Tables 5 and 6, the maximum correlation error, Err0.3V, is smaller than 3.5% for α = 0.4 but as large as 13.9% for α = 0.3. As observed in Fig. 5, most correlation errors occur at low dimensionless total overpotential, 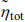 , correspond to the cathode total overpotential range of 0-0.05 V or 0-0.08 V at T = 1000 K. For
, correspond to the cathode total overpotential range of 0-0.05 V or 0-0.08 V at T = 1000 K. For 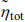 higher than these ranges, the correlation errors are relatively small as shown in Fig. 5. Thus, it may be necessary in future studies to develop a new correlation equation, other than Eq. (18), which is more appropriate for describing the electrochemical effectiveness for current generation in the active reaction layer subject to asymmetric Butler-Volmer reaction kinetics with α < 0.5.
higher than these ranges, the correlation errors are relatively small as shown in Fig. 5. Thus, it may be necessary in future studies to develop a new correlation equation, other than Eq. (18), which is more appropriate for describing the electrochemical effectiveness for current generation in the active reaction layer subject to asymmetric Butler-Volmer reaction kinetics with α < 0.5.
4. Conclusions
In this study, extensive numerical calculations were performed to obtain the electrochemical effectiveness factors for current generation in the active reaction layer of SOFCs. Both the symmetric and asymmetric Butler-Volmer equations were considered to study the charge transfer process by varying the charge transfer coefficient from 0.3 to 0.8. Simple correlation equations were proposed for easy and accurate determination of the numerically determined effectiveness data, and the corresponding correlation coefficients and their estimated errors were summarized. It is anticipated that these results will prove to be useful for estimating current generation in the anodes and cathodes of SOFCs.
Nomenclature
a, b, c, d
Correlation coefficients
F
Faraday constant (96,485 C mol-1)
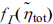
Relative effectiveness factor at finite overpotential of 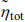
iel
Electronic current density (A m-2)
iex,V
Volume-specific exchange current density (A m-3)
iio
Ionic current density (A m-2)
imax,A
Maximum current density in the active reaction layer (A m-2)
ireal,A
Actual current density in the active reaction layer (A m-2)
itpb
TPBL-specific exchange current density (A m-1)
itr,V
Volumetric charge transfer current density (A m-3)
L
Active reaction layer thickness (m)
ne
Number of electrons for electrochemical reactions (2 for anode, 4 for cathode)
R
Universal gas constant (8.314 J kg-1 K-1)
rp,V
Volume-specific linear polarization resistance (Ω m3)
rtpb
TPBL-specific linear polarization resistance (Ω m)
T
Temperature (K)
z
Coordinate (m)
α
Charge transfer coefficient
ϕT
Thiele modulus
Γeff
Electrochemical effectiveness factor
Γeff,0V
Base effectiveness factor at zero overpotential
η
Activation overpotential (V)
ηconc
Concentration overpotential (V)
ηtot
Total activation overpotential applied to the active reaction layer (V)
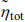
Dimensionless total activation overpotential, 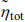 ≡ αneFηtot ⁄ / (RT)
≡ αneFηtot ⁄ / (RT)
φo
Nernst potential (V)
φel
Electronic potential (V)
φio
Ionic potential (V)
λtpb,V
Volume-specific TPBL (m m-3)
σeff
Effective charge conductivity, σeff = (1/σio,eff + 1/σel,eff)-1 (S m-1),
σel,eff
Effective electronic conductivity (S m-1)
σio,eff
Effective ionic conductivity (S m-1)
Acknowledgements
This research was supported by the Daegu University Research Grant (Grant No. 20150130).